Messung der Schallgeschwindigkeit

Euch ist sicher schon einmal aufgefallen, dass der Schall eine bestimmte Zeit braucht, um sich fortzubewegen. Ihr merkt es, sobald jemand ein Geräusch erzeugt, dass weit von Euch entfernt ist und Ihr die Schallquelle seht. Sie bewegt sich, bevor der Schall am Ohr ankommt.

Genau das werden wir nun ausnutzen, um die Geschwindigkeit zu berechnen, mit der sich der Schall ausbreitet. Zunächst überlegen wir uns, wie wir die Geschwindigkeit ausrechnen können. Das kennt Ihr eventuell schon aus Mathe. Die Geschwindigkeit gibt an, wie viel Strecke in einer bestimmten Zeit zurückgelegt wird. Diese Sprechweise führt zur Strecke pro Zeit, was in einer Formel so zu schreiben ist:

Die Geschwindigkeit  hat die Einheit  (Meter pro Sekunde) oder  (Kilometer pro Stunde). Die Strecke  geben wir in  (Meter) und die Zeit  in  (Sekunden). Achtung: Verwechselt nicht die beiden „s“ (Strecke und Sekunden).

Um die Schallgeschwindigkeit zu messen sucht Ihr Euch einen Klassenkameraden und stellt Euch in 300m Entfernung zueinander auf. Einer von Euch klatscht als Signal in die Hände, der andere stoppt die Zeit zwischen dem sichtbaren und dem hörbaren Klatschen.

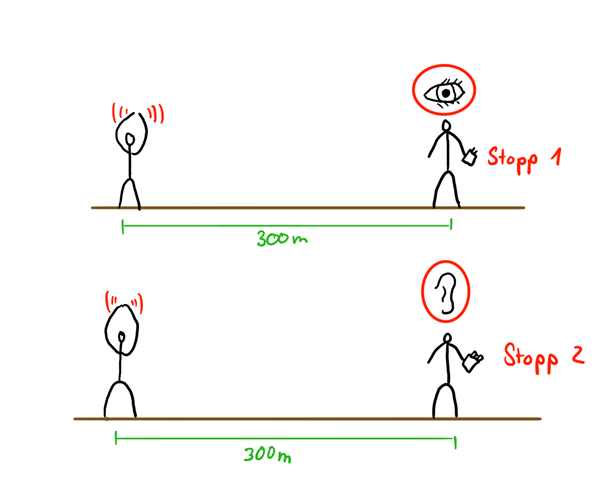
Es könnten zum Beispiel folgende Messwerte entstehen:

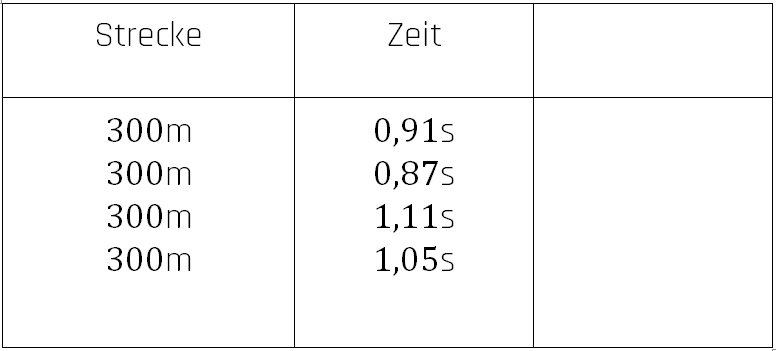
Mit der Formel für die Geschwindigkeit können wir nun die Schallgeschwindigkeit in den verschiedenen Fällen berechnen. Hier eine Beispielrechnung:

Das machen wir für alle Messwerte.

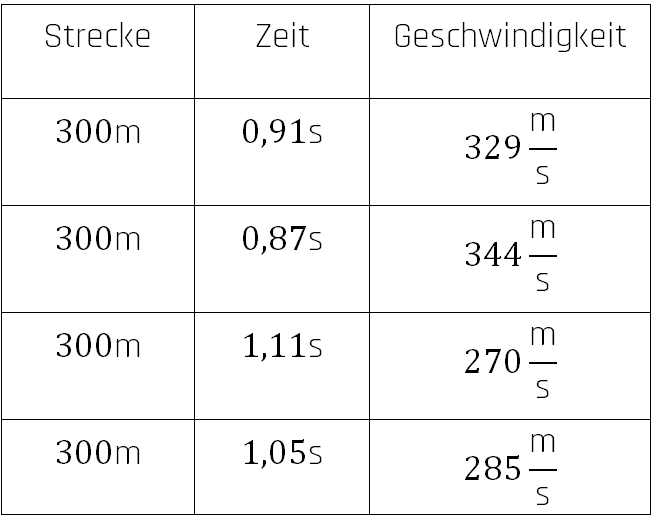
Hiervon bestimmen wir dann den Mittelwert:

Der Literaturwert der Schallgeschwindigkeit in Luft liegt bei: .

Die Schallgeschwindigkeit ist in den verschiedenen Medien unterschiedlich. Habt Ihr schon einmal versucht Euch im Schwimmbad unter Wasser zu unterhalten? Es klingt ganz anders oder? Im Wasser beträgt die Schallgeschwindigkeit ca..

Außerdem ist sie auch abhängig von der Temperatur und der Luftfeuchtigkeit. Sie genau zu messen ist daher schwierig.

Oft gibt man die Abweichung in Prozent an. Dafür teilt Ihr den gemessenen Wert durch den Literaturwert. Der Literaturwert entspricht den 100%:

Das bedeutet, dass die  gerade 90% von den  sind. Also haben wir eine Abweichung von 10%.

Notiz: Es ist auch möglich, dass euer Messwert größer ist, als der Literaturwert. Hier ein Beispiel: .

Das bedeutet, dass die  gerade 107% von den  sind. Die Abweichung liegt also bei 7%.

Als letztes überlegen wir uns, wie wir unsere Messwerte verbessern können:

Wir vergrößern die Strecke s, um die Reaktionszeit zu kompensieren. Die normale Reaktionszeit liegt ungefähr bei . Diese brauchen wir jeweils beim Reagieren auf die Reize „sehen, dass geklatscht wird“ und „hören, dass geklatscht wird“. Da sie nicht immer gleich ist, verfälscht sie das Ergebnis. Ist die gestoppte Gesamtzeit größer, ist das aber nicht so schlimm.

Wir können mehr Messwerte aufnehmen, dann wir der Mittelwert genauer.