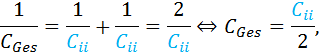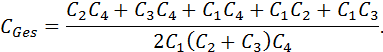Aufgaben

1. Pendel im Kondensator:

     An einem  langem Seil hängt eine geladene Kugel () mit einer Masse von . Im elektrischen Feld wird das Pendel um  ausgelenkt. Bestimme die Stärke des elektrischen Feldes.

2. Die elektrische Feldstärke

     Wie wird die elektrische Feldstärke mit Hilfe der elektrischen Kraft definiert? Gib diese Formel an und stelle sie nach allen möglichen Größen um.

3. Elektronenkanone

     Welche Beschleunigungsspannung muss eine Elektronenkanone bereitstellen, um die Elektronen auf die halbe Lichtgeschwindigkeit zu beschleunigen?

4. Braun’sche Röhre

a. Beschreibe den Aufbau und die Funktion der Braun’schen Röhre und ihrer Bauteile (Natürlich mit Skizze). Zeichne den Kondensator so ein, dass die Feldlinien im Kondensator von oben nach unten verlaufen.

b. Die Elektronen werden mit einer Spannung von  beschleunigt. Welche Geschwindigkeit haben sie, bevor sie in den Kondensator eintreten?

c. Am Kondensator wird eine Spannung von  angelegt. Um wie viel wird ein Elektron im Kondensator in y-Richtung ausgelenkt, wenn die Kondensatorplatten eine Länge von  und einen Abstand von  haben?

d. Die weitere Flugbahn des Elektrons kann durch eine Gerade beschrieben werden. Erkläre warum und berechne die Steigung dieser Geraden.

e. Der Schirm ist  vom Kondensator entfernt. Bei welchem y-Wert trifft das Elektron auf den Schirm?

5. Das elektrische Potential

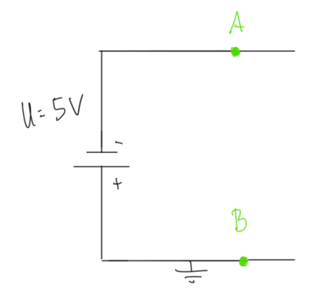
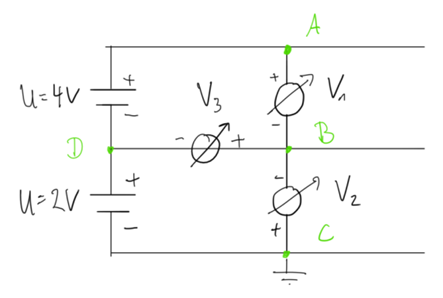
     Gib an den markierten Punkten das elektrische Potential an und berechne die Spannung zwischen den angegebenen Punkten. Sind Spannungsmessgeräte eingezeichnet, dann berechne, welche Spannungen diese anzeigen.

1.)

2.)

6. Kondensator inklusive Ladungsdichte

     Ein Kondensator hat kreisförmige Platten mit einem Radius . Der Plattenabstand beträgt . Bestimme die Kapazität . Nun wird eine Spannung  angelegt. Wie groß ist die Ladung, die auf den Kondensator passt. Wie stark ist das elektrische Feld und wie hoch ist die Flächenladungsdichte?

7. Kondensator mit/ohne Spannungsquelle

     Ein Kondensator () wird an eine Spannungsquelle mit  angeschlossen. Berechne die Ladung .

     Nun wird der Kondensator von der Spannungsquelle getrennt und der Plattenabstand  variiert. Beschreibe und erkläre, ob und wenn ja wie sich folgende Größen verändern:.

8. Kondensator mit Dielektrikum

     Wir betrachten einen mit Luft gefüllten Kondensator. Er ist an eine Spannungsquelle () angeschlossen. Nun verändern wir durch Einbringen eines Dielektrikums die Kapazität. Als Dielektrikum verwenden wir Glas (). Wie verändern sich und ?

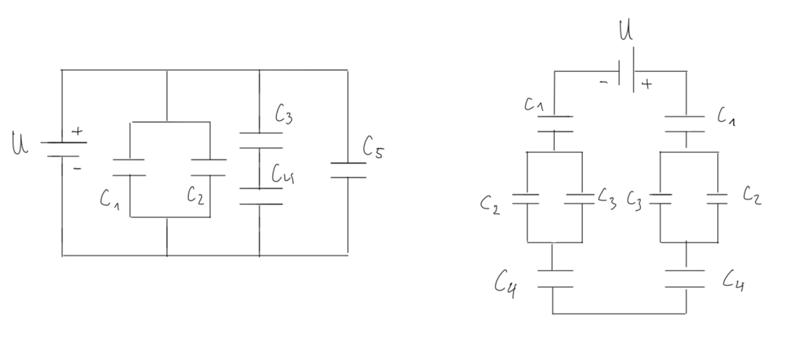
9. Parallel-/Reihenschaltung und Kombination

     Berechne die Ersatzkapazitäten der gegebenen Schaltungen.

Lösungen

1.) Folgende Formel wurde zu diesem Thema hergeleitet:

     Die Herleitung solltet ihr jederzeit abrufen können, denn sie wird auch oft abgefragt. In unserem Fall sind alle Größen bis auf  gegeben.  können wir aber durch

     berechnen. Wir erhalten durch einsetzen:

     Um Rundungsfehler zu minimieren ist es sinnvoll nicht alle Werte einzeln auszurechnen, sondern zuerst die Formeln bis zum Ende umzustellen:

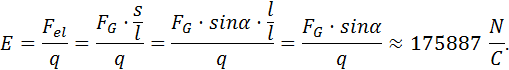
     Rechnet man mit Zwischenergebnissen, dann erhält man folgendes Ergebnis:

     Der Unterschied macht sich durchaus bemerkbar.

     Außerdem fallen oft Größen heraus, wie oben zu sehen. Falls ihr also auf eine Aufgabe stoßt, bei der auf den ersten Blick eine Größe fehlt, kann es sein, dass diese beim Kürzen herausfällt.

2.) Die elektrische Feldstärke wird durch folgende Formel definiert:

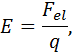
3.)  Beim Beschleunigen der Elektronen wird elektrische Energie in Bewegungsenergie umgewandelt.

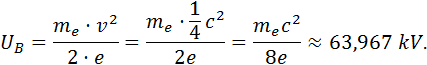
     Notiz: später werdet ihr euch eventuell noch mit der speziellen Relativitätstheorie von Einstein auseinandersetzen. Durch sie müssen wir bei Rechnungen mit hohen Geschwindigkeiten Anpassungen vornehmen. Was bedeutet hier groß? Es muss relativistisch gerechnet werden, sobald die Geschwindigkeit  größer wird als  der Lichtgeschwindigkeit . Dies wäre hier tatsächlich der Fall.

4.) Braun‘sche Röhre

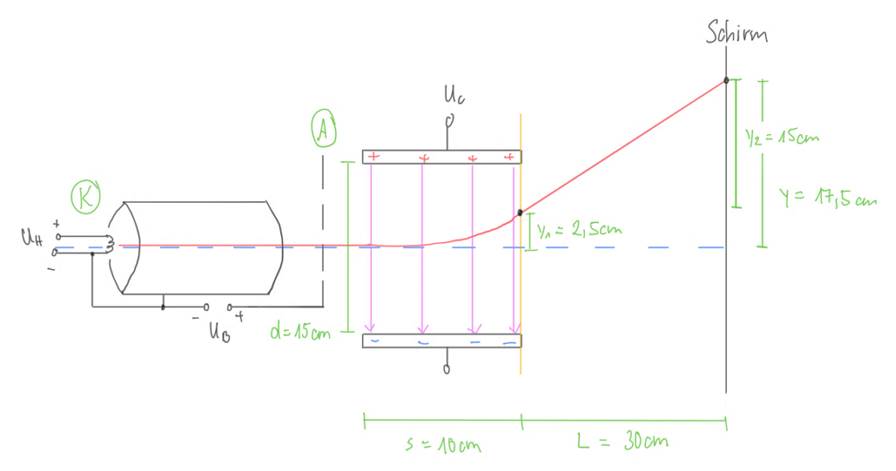
a. Wichtige Bauelemente sind: Heizspirale/Kathode, Wehneltzylinder, Anode, Ablenkkondensator, Schirm. Wichtig ist auch das Einzeichnen der Spannungsquellen.

     Die Heizspirale fungiert als Kathode. Durch das Erhitzen können die Elektronen durch den Potentialunterschied zur Anode herausgelöst und beschleunigt werden.

     Der Wehneltzylinder liegt auf einem negativen Potential und zwingt die Elektronen auf seine Symmetrieachse (Mitte).

     Durch das, vom Kondensator erzeugte, elektrische Feld werden die Elektronen nach oben abgelenkt. Hinter dem Kondensator befindet sich der Leuchtschirm. Nach Verlassen des Kondensators verläuft die Bahn der Elektronen linear.

b. Es gilt:

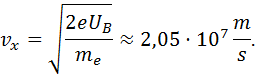
c. Um die Ablenkung zu bestimmen, müssen wir erst wissen wie lange ein Elektron abgelenkt wird – bzw. wie lange es sich im Einfluss des Kondensators befindet:

In dieser Zeit kann das Elektron beschleunigt werden. Die Beschleunigung hierfür resultiert aus der elektrischen Kraft, welche für die Ablenkung verantwortlich ist:

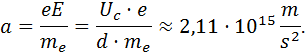
     Die Ablenkung kann nun mit der Formel für beschleunigte Bewegungen ausgerechnet werden:

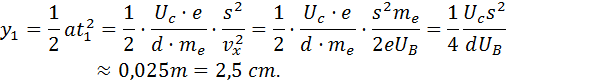
d. Nach Verlassen des Kondensators fällt die beschleunigende Kraft weg, die durch das E-Feld des Kondensators erzeugt wurde. Deshalb behält das Elektron die Richtung bei, die es beim Verlassen des Kondensators hat. Daraus folgt eine Gerade.

     Die Steigung dieser Geraden kann auf zwei Arten bestimmt werden. Die erste Variante (Verhältnisse der Geschwindigkeiten funktioniert nur, wenn der Abstand zum Schirm L gegeben ist. Das ist hier nicht der Fall, so dass wir die Steigung mit Hilfe der Ableitung berechnen müssen. Im Kondensator wird die Bahn des Elektrons durch eine Parabelfunktion beschrieben:

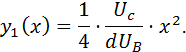
     Das ist die gleiche Formel, die wir zum Berechnen der Austrittshöhe bzw. der Ablenkung verwendet haben, nur dass wir für  ein allgemeines  eingesetzt haben. Die Gerade, die den Verlauf des Elektrons hinter dem Kondensator beschreibt, können wir mit einem bekannten Mittel aus Mathe berechnen: Bestimmung der Tangenten in einem Punkt.

     Eine Gerade hat immer die Form: . In diesem Aufgabenteil wird nur nach  gefragt. Um aber Teil e) zu berechnen ist es sinnvoll die gesamte Geradengleichung zu bestimmen. Die Konstante  können wir aus dem vorangegangenen Aufgabenteil übernehmen:

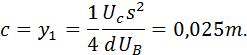
     Es fehlt also . Die Steigung lässt sich mit Hilfe der Ableitung von bestimmen:

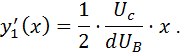
     Benötigt wird die Steigung beim x-Wert . Das ist der Punkt, an dem das Elektron den Kondensator verlässt. Durch Einsetzen folgt

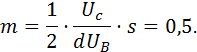
     Es folgt für die Geradengleichung:

e. Durch die Vorarbeit von Aufgabenteil d) können wir den Wert  einfach in unsere Geradengleichung einsetzen um die Höhe auf dem Schirm zu bestimmen:

     Angenommen ihr könnt mit der Ableitung noch nichts anfangen und benötigt noch Übung, dann könnt ihr Aufgabenteil e) auch ohne d) lösen:

     Zuvor haben wir die Beschleunigung durch das E-Feld berechnet, die in y-Richtung wirkt. Hieraus kann auch die Geschwindigkeit in y-Richtung am Endpunkt des Kondensators berechnet werden:

     Die Gesamthöhe kann in zwei Teile unterteilt werden. Der erste Teil beschreibt den Höhenzuwachs im Kondensator  und der zweite Teil beschreibt den Zuwachs zwischen Kondensator und Schirm .

     Zusätzlich zur Geschwindigkeit in y-Richtung können wir berechnen wie viel Zeit das Elektron vom Kondensator bis zum Schirm benötigt:

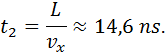
     Jetzt können wir damit  bestimmen:

     Dann erhalten wir folgendes Ergebnis:

5.)  Das elektrische Potential

1. Aufgabenteil:

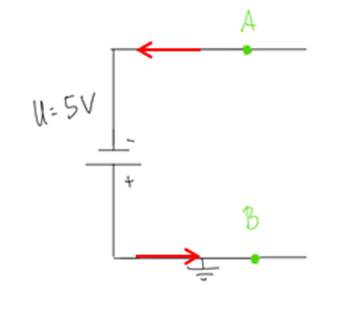
2. Aufgabenteil:

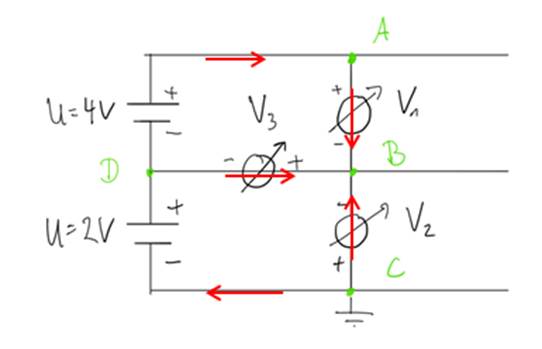
Am besten zeichnet ihr zuerst die technische Stromrichtung ein. Ihr benötigt hier nur die Richtung an den Spannungsmessgeräten, um die angezeigten Spannungen zu berechnen.

6.) Um die Kapazität des Kondensators zu bestimmen, benötigen wir die Fläche seiner Platten:

     Als nächste benötigen wir die Ladung, um alle weiteren Größen berechnen zu können.

      oder

     Der Unterschied der Ergebnisse wird durch Rundungsfehler verursacht.

7.)  Als erstes berechnen wir :

     Trennt man den Kondensator von der Spannungsquellen, dann bleibt die Ladung auf dem Kondensator konstant.

     1. Fall:  wird erhöht. Dann wird  kleiner und  wird größer, da  schließlich konstant bleibt.

     2. Fall:  wird verringert. Dann erhöht sich  und  sinkt, damit  konstant bleibt.

8.)  Durch das Dielektrikum wird die Kapazität verzehnfacht, denn:

     Da der Kondensator an einer Spannungsquelle angeschlossen ist bleibt  konstant. Für  gilt:

     Wir sehen, dass jetzt auch zehn Mal so viele Ladungen auf den Kondensator passen.

9.) Reihen- und  Parallelschaltungen von Kondensatoren

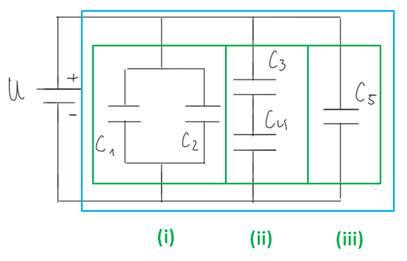
     Um die Ersatzkapazitäten zu berechnen, müsst ihr die Schaltung Stück für Stück vereinfachen, indem ihr immer Teilersatzkapazitäten bestimmt. Wir beginnen mit den grün markierten Kondensatoren:

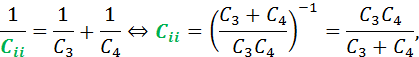
     Als nächstes wird die Parallelschaltung von  bis  durch Addition zusammengefasst:

     Diesen Aufgabenteil könnt ihr auf verschiedene Arten berechnen. Falls ihr das gleiche Prinzip wie in der vorangegangen Aufgabe verwenden möchtet, dann dreht die Schaltung um  nach links und berechnet alles Stück für Stück.

     Einfacher ist die Aufgabe, wenn ihr erkennt, dass es sich insgesamt um eine Reihenschaltung handelt. Zusätzlich sind die beiden Hälften identisch. Es genügt also die Ersatzkapazität einer Hälfte zu berechnen. Zuerst berechnen wir die Parallelschaltung:

     Danach fügen wir die Reihenschaltung einer Hälfte zusammen:

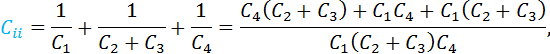
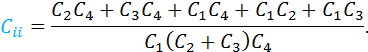
      Danach können wir die Gesamtersatzkapazität bestimmen: