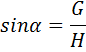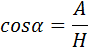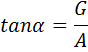Kontrollfragen:

-         Welche Regeln gibt es um Seiten und/oder Winkel im rechtwinkligen Dreieck zu berechnen?

-         Gegeben sind der Winkel  und die Hypotenuse. Wie lautet die Regel zur Berechnung der Ankathete?

 

Lösungen der Kontrollfragen:


Üblicherweise wird dieses Thema behandelt nachdem Ihr den Satz des Pythagoras durchgenommen habt. Sinus, Kosinus und Tangens ergaenzen die Berechnungsmöglichkeiten im rechtwinkligen Dreieck.  Der Satz des Pythagoras gibt Euch eine Möglichkeit die Seiten des Dreiecks zu berechnen. Mit Sinus, Kosinus und Tangens könnt Ihr auch Winkel berechnen oder mit Hilfe eines Winkels Seiten berechnen. Um diese Regel jetzt zu finden schauen wir uns eine zentrische Streckung an.

Die zentrische Streckung verlaengert die Seiten eines Dreiecks so, dass die Winkel des Dreiecks gleich bleiben (siehe ähnliche Dreiecke). Als Beispiel schauen wir uns nun den Winkel  an.

 

 

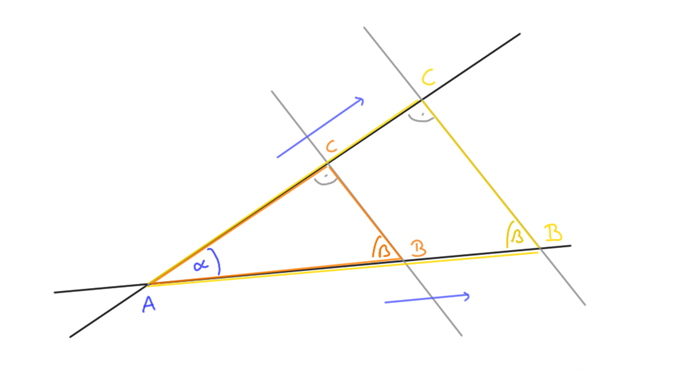
In so einem Fall bietet es sich an, die Seitenverhaeltnisse zu vergleichen. Dann sehen wir, dass wir jedem Winkel ein bestimmtes Seitenverhaeltnis (also eine Zahl)  zuordnen können, z.B.:

 




 

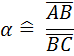
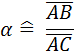
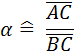
Zur eindeutigen Benennung heißt die Strecke gegenüber vom rechten Winkel Hypotenuse, die Strecke gegenüber vom Winkel  Gegenkathete und die Strecke, die am Winkel  anliegt, Ankathete.

 

 

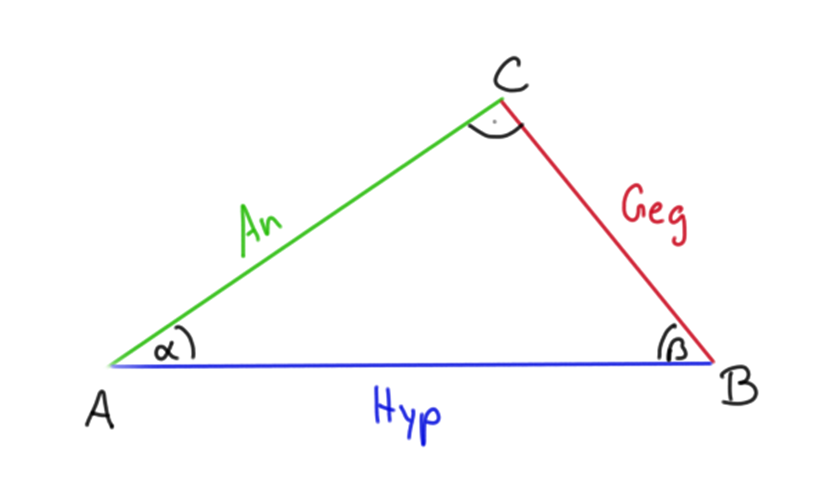
Manche dieser Seitenverhaeltnisse haben Namen. Drei davon sind für Euch in der Schule relevant.

Das erste Verhältnis hat den Namen Sinus von :

 

 

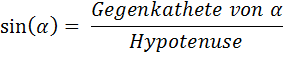
Es gibt noch zwei weitere Seitenverhaeltnisse:

 

 

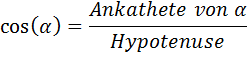
und

 

 

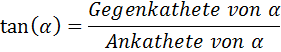
Sie heißen Kosinus und Tangens von α.

 

Wenn Ihr diese Verhaeltnisse auswendig lernt, dann könnt Ihr mit ein bisschen Übung in der Mathearbeit geschenkte Punkte mitnehmen. Im Video gibt es auch ein Rechenbeispiel.

Das mit dem Auswendiglernen ist leichter gesagt als getan. Deshalb hier ein kleiner Merksatz:

„GaGa Hühnerhof AG“: Dies schreibt Ihr dann so auf:

 

 

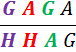
Dann könnt Ihr Sinus, Kosinus und Tangens.

 

Aufgaben:

 

Alle Aufgaben beziehen sich auf ein rechtwinkliges Dreieck mit den Ecken , , , den Seiten , ,  und den Winkeln , , .

1.)    Wie groß ist der Winkel , wenn  und ?

2.)  Wie lang ist , wenn  und ?

3.)  Berechne , wenn und .

4.)  Wie groß ist der Winkel , wenn  und ?

5.)  Wie lang ist , wenn  und ?

6.)  Berechne , wenn  und.

 

Lösungen:

 

1.)     

 


 

 

 

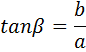
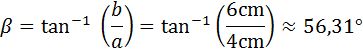
2.)   

 



 

 

 

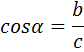
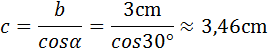
3.)   

 


 

 

 

4.)   

 


 

 

 

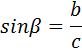
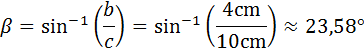
5.)   

 


 

 

 

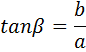
6.)
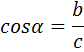